ピアソンとは?
状態:-
閲覧数:2,142
投稿日:2016-05-29
更新日:2016-06-06
カール・ピアソン
・Karl Pearson
・1857年3月27日 - 1936年4月27日
・イギリスの数理統計学者、優生学者で、記述統計学の大成者
2つ以上のもとがあるとき、それらが「どれぐらい類似しているか」という「類似度」を意味する
・2つの変数の間に存在する、直線的関係
「類似度」の強さを「−1から1」までの範囲を取る数字として表現したもの
・ 「変数」と「変数」の類似度を測るための「-1から1」までの値をとる指標
2つのデータセットがある直線に沿ってどの程度沿っているかを示す数値
・「2つの変数の間に存在する、直線的関係」の直線度合い(の絶対値)を「0から1」の数字で表したもの
※「変数」と「変数」の関係が「直線」の場合にのみ、絶対値1(+1 または -1) となる
・Karl Pearson
・1857年3月27日 - 1936年4月27日
・イギリスの数理統計学者、優生学者で、記述統計学の大成者
相関とは?
2つ以上のもとがあるとき、それらが「どれぐらい類似しているか」という「類似度」を意味する
・2つの変数の間に存在する、直線的関係
相関係数とは?
「類似度」の強さを「−1から1」までの範囲を取る数字として表現したもの
・ 「変数」と「変数」の類似度を測るための「-1から1」までの値をとる指標
2つのデータセットがある直線に沿ってどの程度沿っているかを示す数値
・「2つの変数の間に存在する、直線的関係」の直線度合い(の絶対値)を「0から1」の数字で表したもの
※「変数」と「変数」の関係が「直線」の場合にのみ、絶対値1(+1 または -1) となる
公式 / 計算手順
公式
ピアソンの積率相関係数 r = (変数 X と変数 Y の共分散) ÷ ( xの標準偏差 × yの標準偏差 )
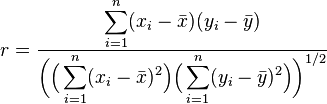
計算手順
1.ユーザABそれぞれの平均点数を求める
総数÷個数
2.ユーザABにおける各レビュー単位での僅差を求める
偏差 = 各レビュー点数 - 平均点
3.ユーザABそれぞれの分散を求める
分散 = 「各レビュー単位での偏差の二乗」の合計 ÷ レビュー数
4.ユーザABそれぞれの標準偏差を求める
標準偏差 = √分散
5.相関係数を求める
相関係数 = 共分散 ÷ ( Aの標準偏差 × Bの標準偏差 )
平均 / 「ピアソンの積率相関係数」算出までの計算例
漫画読者といくつかの漫画に対する彼らの評点ディクショナリ
一覧表
| 漫画 \ 読者 | ブラウン | 麻由 |
|---|---|---|
| キャプテン翼 | 2.5 | 3.0 |
| 北斗の拳 | 3.5 | 3.5 |
| 山田くんと7人の魔女 | 3.0 | 1.5 |
| 君に届け | 3.5 | 5.0 |
| となりの柏木さん | 2.5 | 3.5 |
| ダメな私に恋してください | 3.0 | 3.0 |
| 求める値 | 計算式 |
|---|---|
| 平均 | 読者毎の合計値 ÷ 読者毎の漫画(レビュー)数 |
| 偏差 | 漫画毎の値 – 平均 |
| 分散 | 偏差の二乗の合計÷ 漫画(レビュー)数 |
| 標準偏差 | 分散の平方根(ルート) |
平均
ブラウンの各レビューの平均点数を求める
(2.5+ 3.5 + 3.0 + 3.5 + 2.5 + 3.0) ÷ 6 = 3
→ 平均点数は「3」麻由の各レビューの平均点数を求める
(3.0+3.5+1.5+5.0+3.5+3.0) ÷ 6 = 3.25
→ 平均点数は「3.25」僅差 / 「ピアソンの積率相関係数」算出までの計算例
偏差
上記で求めた平均を各点数から引く
・その値が、各レビュー点数の偏差となる
偏差 = 各レビュー点数 - 平均点
ブラウン偏差 = 各レビュー点数 - 平均点3
麻由偏差 = 各レビュー点数 - 平均点3.25
ブラウンの僅差一覧表
| 漫画 | 僅差式 | 僅差 |
|---|---|---|
| キャプテン翼 | 2.5-平均3 | -0.5 |
| 北斗の拳 | 3.5-平均3 | 0.5 |
| 山田くんと7人の魔女 | 3.0-平均3 | 0 |
| 君に届け | 3.5-平均3 | 0.5 |
| となりの柏木さん | 2.5-平均3 | -0.5 |
| ダメな私に恋してください | 3.0-平均3 | 0 |
| 漫画 | 僅差式 | 僅差 |
|---|---|---|
| キャプテン翼 | 3.0-平均3.25 | -0.25 |
| 北斗の拳 | 3.5-平均3.25 | 0.25 |
| 山田くんと7人の魔女 | 1.5-平均3.25 | -1.75 |
| 君に届け | 5.0-平均3.25 | 1.75 |
| となりの柏木さん | 3.5-平均3.25 | 0.25 |
| ダメな私に恋してください | 3.0-平均3.25 | -0.25 |
分散 / 「ピアソンの積率相関係数」算出までの計算例
分散
標準偏差を求めるために使用
・共分散を求めるためではない!
データの「ばらつき」を表す値
・偏差を二乗した平均を計算することによって求められる
分散 = 偏差の二乗の合計 ÷ アイテム数
ブラウンの分散一覧表
| 漫画 | 僅差の二乗式 | 僅差の二乗 |
|---|---|---|
| キャプテン翼 | -0.5×-0.5 | 0.25 |
| 北斗の拳 | 0.5×0.5 | 0.25 |
| 山田くんと7人の魔女 | 0×0 | 0 |
| 君に届け | 0.5×0.5 | 0.25 |
| となりの柏木さん | -0.5×-0.5 | 0.25 |
| ダメな私に恋してください | 0×0 | 0 |
分散0.16666666666 = (0.25 + 0.25 + 0 + 0.25 + 0.25 + 0) ÷ 6
麻由の分散一覧表
| 漫画 | 僅差の二乗式 | 僅差の二乗 |
|---|---|---|
| キャプテン翼 | -0.25×-0.25 | 0.0625 |
| 北斗の拳 | 0.25×0.25 | 0.0625 |
| 山田くんと7人の魔女 | -1.75×-1.75 | 3.0625 |
| 君に届け | 1.75×1.75 | 3.0625 |
| となりの柏木さん | 0.25×0.25 | 0.0625 |
| ダメな私に恋してください | -0.25×-0.25 | 0.0625 |
分散1.0625 = (0.0625 + 0.0625 + 3.0625 + 3.0625 + 0.0625 + 0.0625) ÷ 6
標準偏差 / 「ピアソンの積率相関係数」算出までの計算例
標準偏差
「標準偏差」の計算は、分散の平方根(ルート)を計算するだけで求められる
標準偏差 = √分散
ブラウン
標準偏差: 0.40824829045 = √0.16666666666
麻由
標準偏差: 1.0307764064 = √1.0625
共分散 / 「ピアソンの積率相関係数」算出までの計算例
共分散
アイテム(ここでは漫画)ごとの x と yの偏差(点数 – 平均)を掛け合わせた平均
相関係数 = 共分散 ÷ ( xの標準偏差 × yの標準偏差 )
漫画読者といくつかの漫画に対する彼らの評点ディクショナリ
一覧表
| 漫画 \ 読者 | ブラウン | × | 麻由 | = | - |
|---|---|---|---|---|---|
| キャプテン翼 | 2.5-平均3 | × | 3.0-平均3.25 | = | 0.125 |
| 北斗の拳 | 3.5-平均3 | × | 3.5-平均3.25 | = | 0.125 |
| 山田くんと7人の魔女 | 3.0-平均3 | × | 1.5-平均3.25 | = | 0 |
| 君に届け | 3.5-平均3 | × | 5.0-平均3.25 | = | 0.875 |
| となりの柏木さん | 2.5-平均3 | × | 3.5-平均3.25 | = | -0.125 |
| ダメな私に恋してください | 3.0-平均3 | × | 3.0-平均3.25 | = | 0 |
0.16666666666=(0.125+0.125+0+0.875-0.125+0)/6
相関係数
相関係数 = 共分散 ÷ ( xの標準偏差 × yの標準偏差 )
相関係数r = 共分散:0.16666666666 /(ブラウン標準偏差: 0.40824829045 × 麻由標準偏差: 1.0307764064) = 0.39605901719・相関係数と順位相関係数について
・解説・講義資料