三角関数とは?
状態:-
閲覧数:2,560
投稿日:2016-11-15
更新日:2017-03-20
Trigonometric functions
・平面三角法における、角の大きさと線分の長さの関係を記述する関数の族および、それらを拡張して得られる関数の総称
三角関数という呼び名
・三角法に由来する
円関数(えんかんすう、英: circular function)と呼ばれることもある
・単位円を用いた定義に由来する呼び名
・平面三角法における、角の大きさと線分の長さの関係を記述する関数の族および、それらを拡張して得られる関数の総称
三角関数という呼び名
・三角法に由来する
円関数(えんかんすう、英: circular function)と呼ばれることもある
・単位円を用いた定義に由来する呼び名
「三角関数」は全部で6種類 /「三角関数の定義」は全部で5種類
「三角関数」は全部で6種類
sin(正弦、sine)
sec(正割、secant)
tan(正接、tangent)
cos(余弦、cosine)
csc(余割、cosecant)
cot(余接、cotangent)
「三角関数の定義」は全部で5種類
A.直角三角形による定義
B.単位円による定義
C.級数による定義
D.微分方程式による定義
E.他の定義
「三角関数」=「直角三角形による定義」ではない
理由
・三角関数は、平面三角法における、角の大きさと線分の長さの関係を記述する関数だけではなく、それらを拡張して得られる関数の総称だから
A.直角三角形による定義
前提
斜辺
・しゃへん
・hypotenuse
・「直角の角」と対向する辺
・直角三角形において、直角と相対する位置にある最も長い辺
隣辺
・りんぺん
・adjacent
・それ以外の辺
・直角三角形において、直角に隣接する2つの辺
・直角三角形の斜辺以外の辺
・ピタゴラスの定理によると、隣辺の二乗同士の和は斜辺の二乗の値と等しくなる
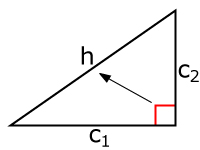
対辺未指定の場合
・下記直角三角形では、斜辺がh、隣辺がc1とc2
対辺
・たいへん
・opposite
・「角度θの角」と対向する辺
「角度θ」とは?
・「不確定の角度」を「θ」と表す
・「不明な長さ」を「x」と表記するのと同じ
概要
直角三角形において、1 つの鋭角の大きさが決まると?
・三角形の内角の和は 180°であることから他の 1 つの鋭角の大きさも決まり、3 辺の比も決まる
∠C を直角とする直角三角形 ABC において、それぞれの辺の長さを AB = h, BC = a, CA = b と表す
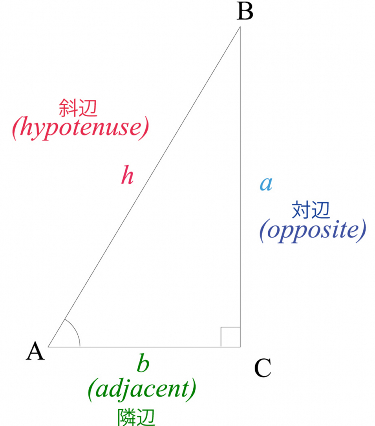
∠A = θ に対して三角形の辺の比 h : a : b が決まる
三角比
三角形の辺の比 が決まると?
・以下6つの値が定まる
正弦(sine; サイン)
sinθ = a/h= 対辺の長さ/斜辺の長さ
正割(secant; セカント)
secθ = h/b = 1/cosθ
正接(tangent; タンジェント)
tanθ = a/b= sinθ/cosθ = 対辺の長さ/隣辺の長さ
余弦(cosine; コサイン)
cosθ = b/h = 隣辺の長さ/斜辺の長さ
余割(cosecant; コセカント)
cosecθ = cscθ = h/ a = 1/sinθ
余接(cotangent; コタンジェント)
cotθ = b/a = 1/tanθ
・三角関数
・円周上の座標(x,y)を求めたいのですが、三角関数の公式は、誰がいつどこで決定したのでしょうか?"